JModelica.org 使い方メモ
Table of Contents
はじめに
JModelica.org は、Modelica 言語に基づいて複雑な動的システムのモデル化、シミュレーション、最適化および分析などを行うプラットフォームとなるソフトウェアです。モデルは Modelica 言語で記述しますが、オペレーションのほとんどは Python を使用して行います。Lund 大学などの学術機関と民間企業の協力を得て、Modelon AB によってオープンソースソフトウェアとして維持開発されてきました。Modelon は、2019年12月18日に、Assimulo, PyFMI, FMI Library を除くコンパイラや最適化機能など含む部分を一般に使用可能なオープンソースとすることを止めてしまいました。今後も商用および学術的用途で利用されるソフトウェアとして開発は続けられるそうです。
現在、https://jmodelica.org/ のフォームに登録することによって、最後のオープンソースバージョンのソースコードと Windows用バイナリのダウンロードが可能です。この Windows 用バイナリ JModelica.org-2.14.exe には Jupyter Notebook が含まれていてすぐ利用することができます。また、Mac でも、Docker コンテナに JModelica.org と Jupyter Notebook をインストールすることによって同様の環境を構築することができます。
Jupyter Notebook を使うと、モデルの作成、シミュレーションの実行、結果の図化などのオペレーションの履歴をファイルに保存して再利用することができます。また、Github Gist を利用して作成したファイルを公開することができます。以下、このようにして作成した JModelica.org の使い方のメモを示します。自分用のメモとして随時追記します。
JModelica.org を Jupyter Notebook から利用する
Windows の場合
- JModelica.org-2.14.exe をダブルクリックしてインストールします。
- ホームディレクトリ C:\Users\ユーザー名 に jmodelica という名前のフォルダを作ります。
- C:\JModelica.org-2.14\IPython64.bat をコピーして以下のようなバッチファイル jm_start.bat を作成します。
@echo off call C:\JModelica.org-2.14\setenv.bat 64 if %errorlevel% neq 0 pause cd %USERPROFILE%\jmodelica "%PYTHONHOME%\python.exe" -m jupyter notebook %* if %errorlevel% neq 0 pause
このバッチファイルをダブルクリックで実行すると、ブラウザが起動して Jupyter Notebook が使用できます。New > Python 2 を選択してセルに、次のように入力してシフト＋リターンを押します。
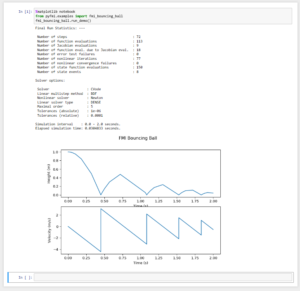
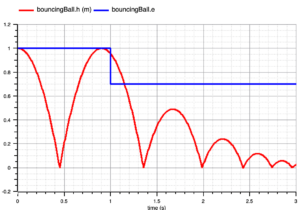
%matplotlib notebook from pyfmi.examples import fmi_bouncing_ball fmi_bouncing_ball.run_demo()
同様に次のように入力します。
# Import and run the CSTR example using CasADi and plot results from pyjmi.examples import cstr_casadi cstr_casadi.run_demo()
# Import the RLC example from pyjmi.examples import RLC # Run the RLC example and plot results RLC.run_demo()
Dymat と Pandas をインストールします。DyMat は JModelica, Dymola, OpenModelica などの mat ファイルを読み込んだり、他のファイル形式にエクスポートすることができるライブラリです。Pandas はデータ解析を支援するライブラリです。便利なのでこれらをインストールします。
pip のアップデート
%%system pip install --upgrade pip
DyMat のインストール
%%system pip install DyMat
Pandas のインストール
%%system pip install pandas
Mac の場合
JModelica.org の Docker イメージを作って Jupyter Notebook で利用する に示しました。
以下は、Mac を使用して作成しました。
簡単なモデルを作ってシミュレーションを実行する
モデルを作ってシミュレーションを実行する
DyMat を使ってシミュレーション結果を読み込む
モデルに入力信号を設定してシミュレーションを行う
モデルのパラメータを変えたシミュレーションを行う
VDP_with_sweep_parameters.ipynb
Package 内の Class のシミュレーションを実行する
Modelica Standard Library を使用する
Modelica.Mechanics.Rotational.Examples.First
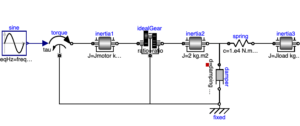
このモデルは、正弦波的に変動するモーターのトルクによって駆動されるドライブトレイン（自動車などの動力伝達系)を表しています。
First.ipynb
OpenModelica による計算結果
Modelica.Fluid.Examples.Tanks.EmptyTanks
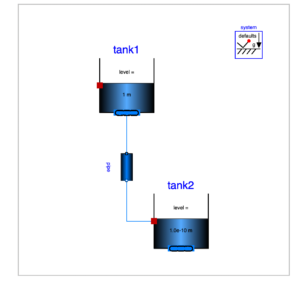
このモデルは、上下に配置されたタンクをパイプで繋いだ状態を表しています。上のタンク(tank1)から下のタンク(tank2)へパイプを経て水が移動します。
この例題では、デフォルトのソルバー CVode ではシミュレーションできないので LSODAR に変更します。JModelica で Fluid パッケージを計算する を参照して下さい。
オプション設定の詳細は、JModellica.org User Guide – Version 2.10 の 5.3.2.2 Options for Model Exchange FMUs を参照してください。
EmptyTanks.ipynb
OpenModelica によるシミュレーション結果
入力信号のあるエンジンモデル
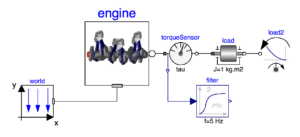
JModelica User Guide – Version.2.10 5.4.3. Simulation of an Engine model with input のシミュレーションを実行します。このモデルは、MSLの例題 Modelica.Mechanics.MultiBody.Examples.Loops.EngineV6_analytic のエンジン負荷となるトルクコンポーネントを、回転数から計算する QuadraticSpeedDependentTorque から、外部入力信号で設定可能な Torque に変更したものです。外部入力信号は Python の関数で定義します。
OMEdit などの GUI は使用せずにテキストベースで作成するので、コンポーネントの配置に関する情報は含んでいません。
MSLのEngineV6_analytic（改変前のモデル）
Modelica.Media を使って室温の変化を調べる
これは、1. Modelica のクラスの概要 の ClassExample9 として、 Modelica.Media の BaseProperties モデルの使い方を示すために作成した例題です。
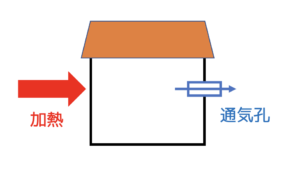
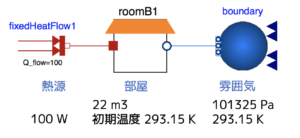
- 圧力を一定に保った部屋を加熱します。
- 部屋には通気孔があり、膨張した空気が流出します。
まず単体で動作するモデルを作成します。次にこれをコンポーネント化して熱流量や圧力を外部のコンポーネントから与えられるようにします。
RoomA (単体モデル)
RoomB (コンポーネント化したモデルのテスト)
OpenModelica によるシミュレーション結果
Third Party Library を使用する
Modelica Standard Library 以外のライブラリの使用方法は、
- 環境変数 MODELICAPATH にライブラリを配置したパスを設定する方法
- compile_fmu の引数のファイル名として、ライブラリのファイル名やディレクトリ名をフルパスで設定する方法
があります。ここでは前者の方法を用います。
Buildings.Examples.Tutorial.SpaceCooling.System3
LBNL の Modelica Buildings Library の例題 System3 を実行します。
- Download から、Buildings-v6.0.0.zip をダウンロードします。
- Mac の場合 /Users/ユーザー名/jmodelica/lib で解凍します。
- Windows の場合 C:\Users\ユーザー名\jmodelica/lib で解凍します。
ライブラリのディレクトリが、Mac と Windows でそれぞれ
- /Users/ユーザー名/jmodelica/lib/Buildings 6.0.0
- C:\Users\ユーザー名\jmodelica\lib\Buildings 6.0.0
となることを想定しています。
Buildings.Examples.Tutorial.SpaceCooling.System3
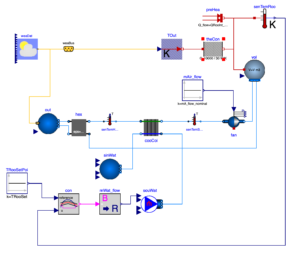
熱伝導や換気によって夏の外気と熱のやりとりをする室内を、水冷式のコイルクーラーで冷やすモデルです。クーラーの冷却水の流量を、室温センサーを使用した制御回路でオンオフを制御します。
ThermoPower.Test.GasComponents.TestCC
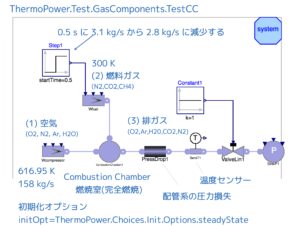
ThermoPower ライブラリに含まれる CombustionChamber (燃焼室)のテストモデル TestCC のシミュレーションを実行します。
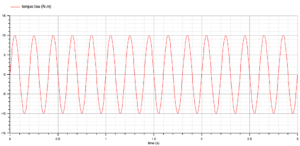
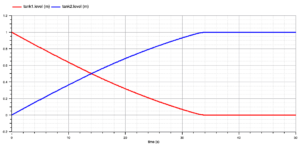
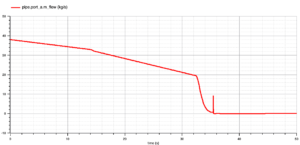
このモデルは、コンプレッサから出た空気(Compressor Air)と燃料ガス(Fuel Gas)が燃焼室で混合し、燃焼ガスに含まれる CH4 が完全燃焼する現象をモデル化しています。そして、発熱によって加熱された排ガス(Exhast Gas)が排出されます。燃焼による発熱量は、燃焼室のモデルパラメータとして低位発熱量(Lower Heating value of fuel) HH = 41.6e6 J/kg を与えています。0.5秒に燃料ガスの質量流量を 3.1 kg/s から 2.8 kg/s に減少させます。モデルについて調査した概要は、
に解説を書きました。
TestCCの概要
ThermoPower ライブラリを GitHub mirror や svn://svn.code.sf.net/p/thermopower/svn/trunk から入手して、ライブラリのディレクトリが、Mac と Windows の場合、それぞれ、
- /Users/ユーザー名/jmodelica/lib/TermoPower 3.1
- C:\Users\ユーザー名\jmodelica\lib\ThermoPower 3.1
となることを想定しています。
TestCC_includeEOF – 反応物と生成物の生成エンタルピーの差から発熱量を計算する
上述のTestCCでは、燃料ガスの低位発熱量 (Lower Heating Value of fuel) をパラメータとして設定することによって、発熱量を計算しました。このモデルは、すべての Media (物性モデル) の生成エンタルピを除外するパラメータ excludeEnthalpyOfFormation を false にし、低位発熱量 HH=0 を設定することによって、反応物と生成物の生成エンタルピーの差から発熱量を求めるように変更することができます。このような改造を行ったモデル TestCC_includeEOF を作成してシミュレーションを行います。
Functional Mock-up Interface (FMI) を使用する
FMU の生成とシミュレーションの実行
Functional Mock-up Interface (FMI) は、様々なダイナミックシステムのシミュレーションツール間でモデル交換や Co-Simulation を行うための規格です。規格書はhttps://fmi-standard.org/downloads/ からダウンロードできます。FMI をサポートするツールのリストが https://fmi-standard.org/tools/ にあります。
JModelica.org を使用すると、
- FMI Version 1.0 Model Exchange (ME10)
- FMI Version 1.0 Co-Simulation (CS10)
- FMI Version 2.0 Model Exchange (ME20)
- FMI Version 2.0 Co-Simulation (CS20)
に従った Functional Mock-up Unit (FMU) を生成することと、FMUを読み込んでシミュレーションを実行することができます。ここでは、これらの FMU の生成とシミュレーションを行います。
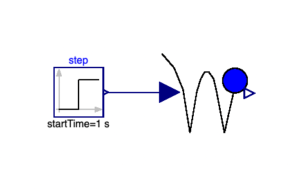
OpenModelica で同様なシミュレーションを行った結果を以下に示します。このモデルはBouncingBallモデルの入力信号を Modelica.Blocks.Sources.Step で生成しました。
OpenModelica で作成したモデル
FMI1.0 CS の Co-Simulation を行う
FMI_BouncingBall.ipynb では、BouncingBallモデルの入力信号である反発係数をPythonの関数で作成しました。この反発係数を出力する部分を Modelica.Blocks.Sources.Step でモデル化し、FMUを作成します。
FMI1.0 for Co-Simulation の簡単な例として、この反発係数を出力するモデル (model1) とBouncingBallモデル (model2) の２つのサブシステムモデルがデータ交換を行う Co-Simulation モデルを Python スクリプトで構成します。
FMI1.0 for Co-Simulation については、
- Functional Mock-up Interface for Co-Simulation Document version: 1.0.1, Modelica Association Project FMI
- FMI1.0 FMI for Co-Simulation について
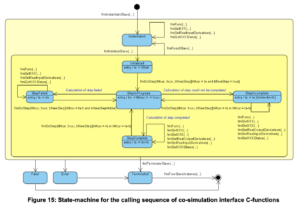
を参照してください。前者は、FMI1.0CS の仕様書です。p.30 にサブシステムモデルの状態遷移図があります。
FMI1.0CSのモデルの状態遷移図
この例題ではPython スクリプトを用いて、load_fmu でサブシステムをインスタンス化し、モデルの状態を遷移させる関数（initialize, do_stepなど) やデータ交換関数(get, set など) を使用して Co-Simulation プロセスを実現します。
FMI2.0 CS の Co-Simulation Master 機能を使ってみる
BouncingBall の例題
JModelica.org には、FMI2.0 CS の規格の FMU を読み込んで Co-Simulation モデルを構築する Master ツールの機能があります。この機能を使用して FMI10CS_BouncingBall.ipynb と同様の Co-Simulation モデルを作成します。
GenerationOfFMUs
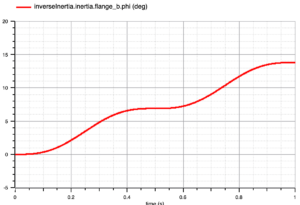
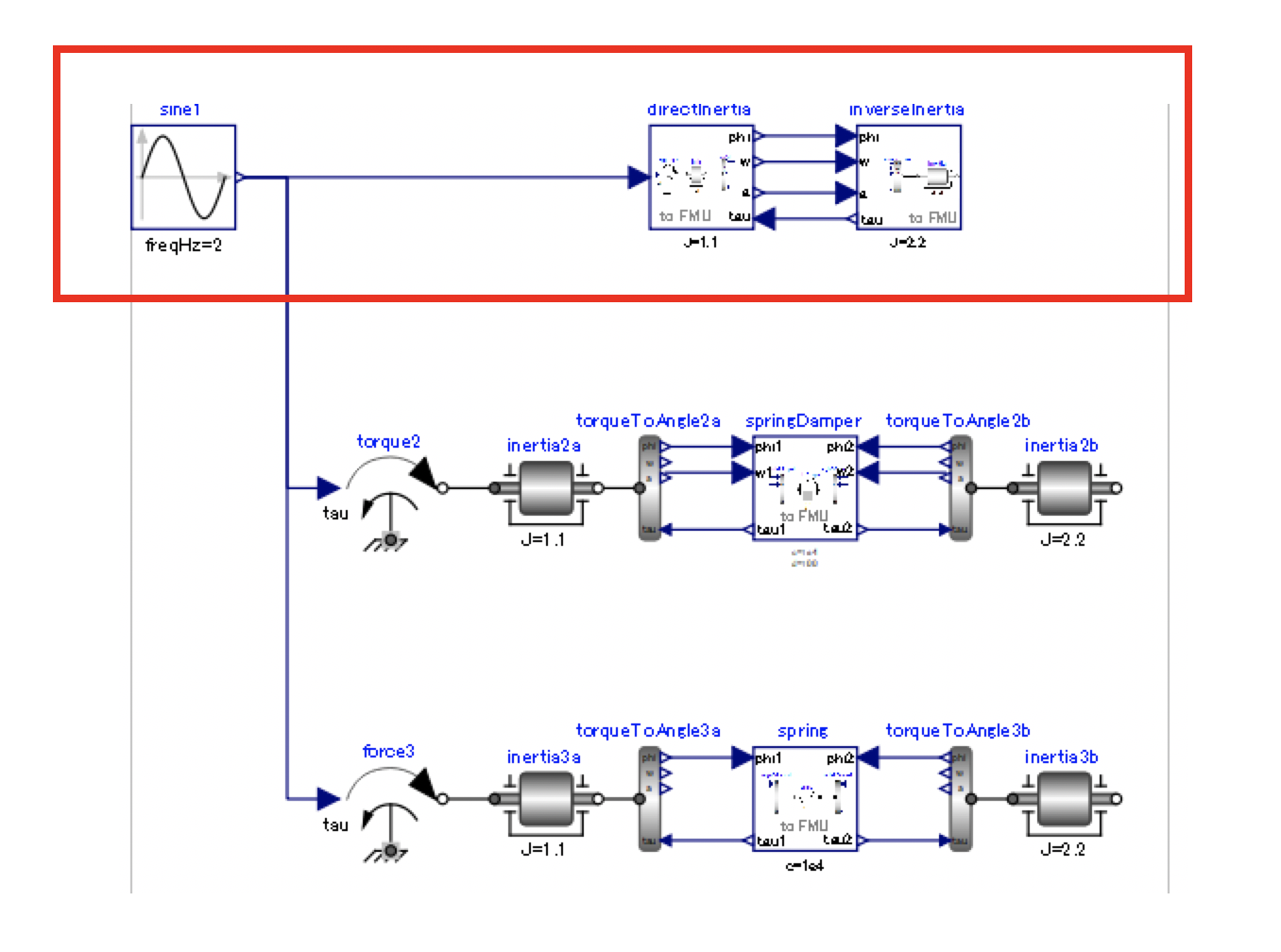
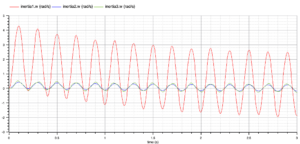
下図は、OpenModelicaで、MSLのModelica.Mechanics.Rotational.Examples.GenerationOfFMUsのシミュレーションを行った結果の inverseInertia.flange_b.phi です。
inverseInertia.inertia.flange_b.phi
MSLのGenerationOfFMUs
Modelon の資料 CO-SIMULATION USING THE OPEN-SOURCE PYTHON PACKAGE PYFMI は、このモデルの一部（赤で囲んだ部分）を FMU の Co-Simulation で表したモデルの例題です。この資料の手順でシミュレーションを行ってみます。
GenerationOfFMUs_without_linear_correction.ipynb
GenerationOfFMUs_with_linear_correction.ipynb
結局 JModelica.org で生成した FMU2.0CS の fmu では directional derivative がサポートされないため正しく計算できませんでした。
このモデルでは、linear_correction = True にしないと正しい計算が行えませんが、そのためには FMUが directional derivative をサポートする必要があります。調べてみると、JModelica.org version.2.2 の Release Note に
- Removed the experimental directional derivative generation feature.
という記述があり、以後のバージョンでは使用できません。また、Directional derivatives in JModelica FMUs – Stack overflow によると JModelica.org では使えないが、OPTIMICA Compilerでは使えるという情報がありました。
OpenModelica で directional derivative を有効にしたFMUを作成することは可能ですが JModelica.org では読み込めませんでした。
微分代数方程式系 (DAEs) の動的最適化を行う
JModelica.org の動的最適化(dynamic optimization)機能には
- CasADi による direct collocation を用いた微分代数方程式系 (DAEs) の動的最適化 (dynamic optimization)
- FMUを用いた常微分方程式系の微分を使わないキャリブレーションや最適化
が行えます。ここでは前者の例題を示します。
Van der Pol oscillator モデルの動的最適制御
簡単な微分代数方程式系の一例として Von der Pol oscillator モデルを用い最適制御の方法を示します。JModelica.org Users Guide – Version 2.10 6.2 の例題の実習です。
連続撹拌反応槽 (CSTR) の動的最適制御
Modelica 言語で作成したモデルを用いた最適制御の方法を示します。JModelica.org Users Guid – Version 2.10 6.5.2.1 の例題の実習です。
CSTR_dynamic_optimal_control.ipynb
目的地への到達時間が最小になるように制御する
JModelica.org Users Guide – Version 2.10 6.5.2.2 Minimum time problem を実習します。この例題は、Docker で Ubuntu のバイナリを実行する Mac の環境ではエラーになってしまいました。 Windows版のみで成功しました。制御対象の微分代数方程式モデルは制御信号付きの Van der Pol oscillator を使用し、状態変数が初期値から与えられた目的の値に変化する時間が最小になるように、モデルを制御します。
4つのタンクに液体を分配するシステムのパラメータを推定する
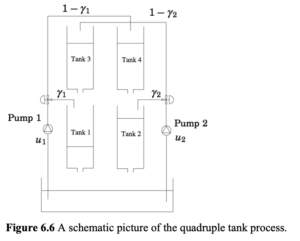
JModelica.org Users Guide – Version 2.10 6.5.2.4. Parameter estimation の例題を実習します。
このシステムは、ポンプ２個、３方型バルブ２個、タンク４個から構成されています。ポンプ１から送られた液体は、分岐してタンク１とタンク４に注がれ、ポンプ２から送られた液体は分岐して、タンク２とタンク３に注がれます、タンクの底には穴が空いていて液体が流出します。タンク１の上にタンク３が配置されており、液体がタンク３からタンク１に流れ込みます。同様に、タンク２の上にタンク４が配置されていおり、タンク４からタンク２に液体が流れ込みます。ポンプの流量は電圧を加えることによって制御します。
タンク１〜タンク４の液位を状態変数とし、ポンプの電圧を制御変数として、このタンクシステムをモデル化します。タンクの液位とポンプの電圧の時系列の測定データを元にして、測定データとシミュレーション結果が合うようなモデルパラメータを推定します。
Quadruple Tank System, JModelica.org Users Guide より
FMUを用いたモデルのキャリブレーションや最適化を行う
Modelica.org の動的最適化(dynamic optimization)機能には
- CasADi による direct collocation を用いた微分代数方程式系 (DAEs) の動的最適化 (dynamic optimization)
- FMUを用いた常微分方程式系の微分を使わないキャリブレーションや最適化
が行えます。ここでは後者の例題を示します。
古田の振り子のモデルパラメータのキャリブレーションを行う
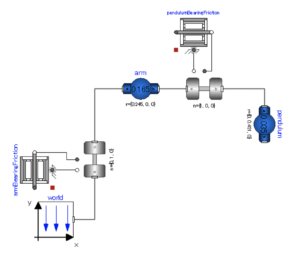
JModelica.org Users Guide – Version 2.10 6.6. Derivative-Free Model Calibration of FMUs の実習を行います。
古田の振り子 (Furuta pendulum) は、水平面内で回転するアームとアームに対して垂直な面内で自由に回転する振り子から構成されています。アームの回転角度 phi とアームと振り子の間の回転角度 theta の２つの自由度があります。MSL の MultiBody ライブラリを使って作成された古田の振り子のモデル Furuta.mo が、JModelica.org の例題に含まれています。モデルと OpenModelica によるシミュレーション結果のスクリーンショットを示します。
古田の振り子のモデル Furuta.mo
OpenModelica によるシミュレーション
この例題では、実験で測定した phi と theta の値を用いて、モデルのパラメータであるアームの摩擦トルク係数 armFriction と振り子の摩擦トルク係数 pendulumFriction を求めます。最適化アルゴリズムはNeider-Mead simplex optimization algorithm を使用します。
