熱力学とエネルギー(1)　[執筆中]

現代社会に生きる我々にとってエネルギーという概念は身近です．日常的にエネルギーと言われているものは，電気やガスやガソリンなどの形で提供され，ものや情報を搬送する動力や，ものを温める熱，照らす光として使用されます．

本記事では，何回かに分けてエネルギーをメインテーマとして熱力学を復習したいと思います．目標としては，最終的には Modelica の Media モデルの作り方に到達したいと思います．

申し訳ありませんが，まだ未完成です．あとエントロピーの解説を行う予定です．

記事が長くなりすぎたので分割します．

1. 物理学的なエネルギー

1.1 エネルギーと仕事

物理学では，エネルギー (energy) はなんらかの形で物体や系に蓄えられたや仕事をする能力を表します．外部から物体に作用する力（外力）を $\boldsymbol{f}_{ex}$[N] とし，力の向きに物体の位置が $\boldsymbol{x}_1$ [m]から$\boldsymbol{x}_2 (>\boldsymbol{x}_1)$ [m]まで移動したとき，外力によって物体がなされた仕事 (work) は，

$$W (\boldsymbol{x}_1 \rightarrow \boldsymbol{x}_2) = \int_{\boldsymbol{x}_1}^{\boldsymbol{x}_2} \boldsymbol{f}_{ex} \cdot d \boldsymbol{x} \ {\rm [J]} \tag{1}$$

となります．このとき物体は反作用により $- \boldsymbol{f}$ の力で外部を押し返しています．つまり物体が外部に対してした仕事は $-W(\boldsymbol{x}_1 \rightarrow \boldsymbol{x}_2)$ [J] です．ややこしい表現ですが，エネルギーは物体がした仕事 $-W(\boldsymbol{x}_1 \rightarrow \boldsymbol{x}_2)$ [J] の分だけ減少した，言い換えると，物体がなされた仕事 $W(\boldsymbol{x}_1 \rightarrow \boldsymbol{x}_2)$ [J] の分だけ増加したといえます．物体や系のエネルギーの変化量は，最終的には，外部から物体や系がなされた仕事の量で表現することができ，仕事と同じ J (ジュール）= Nm という単位を使って表します．すなわち，物体のエネルギーの変化量を $\Delta E \ {\rm [J]}$ とすると，

$$\Delta E = W (\boldsymbol{x}_1 \rightarrow \boldsymbol{x}_2) \tag{2}$$

となります．

1.2 系とエネルギー

熱力学では，考察の対象とするものを系 (system) といい，系を除くものを外界 (environment または surroundings) といいます．系が外界に正の仕事をすると系のエネルギーが減少し，外界が系に正の仕事をすると系のエネルギーが増大します．系という概念は，物体や複数の物体の集まりを表すだけではなく，空間にアイデンティティを置く場合もあります．例えば，シリンダの中の空気やパイプ内部の水を系と考える場合，中身の空気や水が出入りして最初とは全く別のものに変わっても同じ系の状態が変化したとみなします．また，容器内部の真空状態を表すような物質がまったく無い系も考えられます．系の概念では，物質の量は状態変数の一つであり，系の中にある物質の量が変化しないように制御された系を閉じた系 (closed system) といいます．物体は閉じた系に近いものです．物体の概念では物質の量は物体に固定された属性です．力学では主に物体のエネルギーを扱い，熱力学では系のエネルギーを扱います．

系と物体では，エネルギーの概念が若干異なります．エネルギーを変化させる方法は，物体では仕事でしたが，系では仕事のみではなく加熱する方法や系に含まれる物質の量を変化させる方法などもあります．また，系が持っているエネルギーを全て仕事として取り出せるわけではありません．エネルギーの移動を定量化するには，仕事以外のエネルギー移動形態を含めて議論する必要があります．

2. 物体のエネルギー

まず，物体のエネルギーについて概観します．ここでポテンシャルエネルギーや保存力を紹介するのは，後述する熱力学的な状態量の説明で，ポテンシャルエネルギーと類似した概念を使用するためです．ただし大きな違いもあります．それは，ポテンシャルエネルギーは位置 $\boldsymbol{x}$ の関数ですが，熱力学的な状態量は圧力 $p$，体積 $V$，温度 $T$ などの熱力学的状態変数の関数であることです．また，熱力学でも，ここで紹介するエネルギー保存則の概念は重要です．そもそも，冒頭で述べた物体や系に仕事をするとエネルギーが増大するという考えは，物体や系にエネルギーが蓄えられるという考えに基づいています．

質量 $m$ の物体の重心の運動状態は，

• 位置 (position)
• 速度 (velocity) または運動量 (momentum)

で表すことができます．物体の力学的なエネルギーには，

• ポテンシャルエネルギー (potential energy)
• 運動エネルギー (kinetic energy)

があります．

2.1 ポテンシャルエネルギー (potential energy)

力を $\boldsymbol{f}_p$，エネルギーを $E_p$とすると，　

$$\boldsymbol{f}_p = -{\rm grad} \ E_p = – \left( \frac{\partial E_p}{\partial x}, \frac{\partial E_p}{\partial y} , \frac{\partial E_p}{\partial z} \right) \tag{3}$$

のように表せるとき $E_p$ をポテンシャルエネルギー (potential energy) といい， $\boldsymbol{f}_p$ を保存力 (conservation force) といいます．物体が外部からされる仕事を微分で表すと，

$$ dW = \boldsymbol{f}_p \cdot d \boldsymbol{x} = -{\rm grad} \ E_p \cdot d \boldsymbol{x} = – \left( \frac{\partial E_p}{\partial x} dx + \frac{\partial E_p}{\partial y} dy + \frac{\partial E_p}{\partial z} dz \right) = – dE_p \tag{4}$$

となります．このように仕事の変化が変数の全微分で表せる場合，任意の位置 $A$ から出発して任意の経路で物体を移動させて $A$ に戻ると物体が外部からされた仕事はゼロとなります．この閉じた経路を $C$ で表すと，

$$ W = \oint_C dW = 0 \tag{5}$$

のように書けます．この場合，

$$ W(\boldsymbol{x}_0 \rightarrow \boldsymbol{x}) = \int_{\boldsymbol{x}_0}^{\boldsymbol{x}} dW \tag{6}$$

は，経路によらず始点 $\boldsymbol{x}_0$ と終点 $\boldsymbol{x}$ の関数となります．(4)のように全微分で表せることと (5),(6)は同値な関係です．

ポテンシャルエネルギーの具体例を見ていきましょう．

重力による位置エネルギー (gravitational potential energy)

3次元直交座標系の位置は $\boldsymbol{x} = (x,y,z)$, 重力は $\boldsymbol{f}_g = (f_{gx}, f_{gy}, f_{gz})=(0,0,-mg)$ のように表せます．重力が $z$ 成分のみしかないので，単純化して $z$ 方向のみの式で表します．　

質量 $m$ の物体を，高さ $z_1$ [m]から $z_2 (> z_1)$ [m] に持ち上げる場合を考えます．重力 $f_{gz}= – mg$ に抗して外力 $f_{ex} = mg$ を加えます．物体が外部からされる仕事は，

$$W(z_1 \rightarrow z_2) = \int_{z_1}^{z_2} f_{ex} dz = mg　(z_2-z_1) >0 \tag{7}$$

となります．逆に $z_2$ から $z_1$ に物体を落下させる場合は，$W(z_2 \rightarrow z_1) = -W(z_1 \rightarrow z_2) <0$ [J] となります．これらの仕事によって変化するエネルギーを $E_g$ とします．つまり仕事からエネルギーを定義します．

$x_1$ から $x_2$ に持ち上げるときの $E_g$ の変化は，

$$ \Delta E_g = W (z_1 \rightarrow z_2)= mg(z_2 – z_1) \tag{8}$$

です．$z_0 = 0$ を基準点とするとエネルギーは，

$$ E_g = W(z_0 \rightarrow z) = mgz \tag{9}$$

と表せます．

３次元に座標系にして，(3) のように $E_g$ の勾配を求めると，

$$\boldsymbol{f}_g = -{\rm grad} \ E_g = -\left( \frac{\partial E_g}{\partial x}, \frac{\partial E_g}{\partial y}, \frac{\partial E_g}{\partial z} \right) = (0,0,-mg) \tag{10}$$

となるので，$E_g$ はポテンシャルエネルギーであり，重力 $\boldsymbol{f}_g = (0,0,-mg)$ は保存力です．

$$ dW =- dE_g = – \frac{\partial E_g}{\partial x} dx – \frac{\partial E_g}{\partial y} dy – \frac{\partial E_g}{\partial z} dz = mg \ dz \tag{11}$$

となり，これを $z$ 方向に積分したものが(7) となります．　

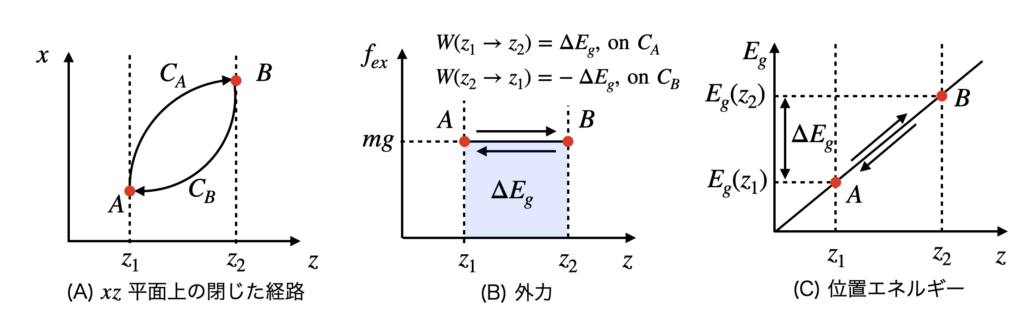
例として物体が $xz$ 平面上を移動する場合を考えます．図1(A) は物体を $A$ から $B$ へ移動させる経路 $C_A$ と $B$ から $A$ へ戻す経路 $C_B$ を示したものです．$z$ 軸は，高さ方向を表すので普通の感覚では縦軸にしますが，ここでは(B)(C)と合わせて横軸にしました．(B) は縦軸が外力 $f_{ex} = -f_{gz} = mg$ です．外力の$z$ 方向以外の成分は物体の移動には必要ないのでゼロです．物体は，$C_A$ では $\Delta E_g >0$ (薄い青色部分の面積）の仕事をされ，$C_B$ では $- \Delta E_g < 0$ の仕事をされます．位置エネルギーは (C) のように $\Delta Eg$ だけ増大してからまた元にもどります．$C_A$ と $C_B$ からなる閉じた経路で物体がされる仕事はゼロとなり，(5)が成り立ちます．

ばねによる弾性エネルギー (elastic energy)

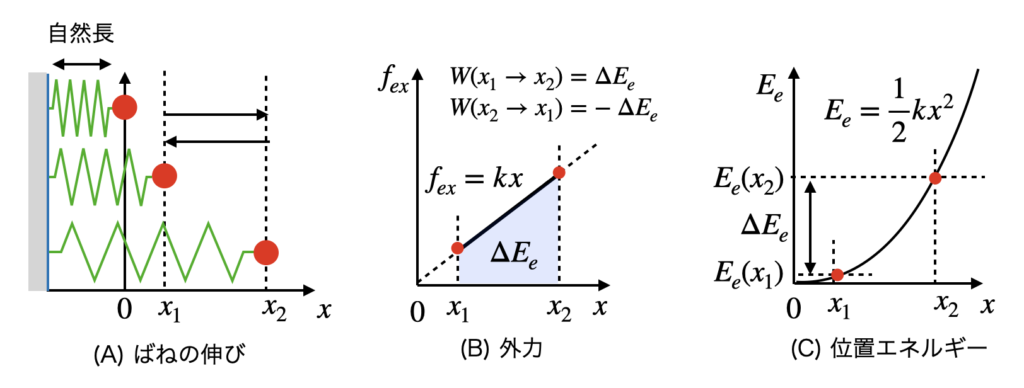
図2(A)のように一端が固定されたばねの他端に接続された物体あり，ばねの伸びを $x = l – l_0 \ {\rm [m]}$とします．$l$ はばねの長さ，$l_0$ はばねの自然長です．ばね定数を $k {\rm [Nm]}$とすると弾性力は $f_e = -k x {\rm [N]}$ となります．ばね伸びを $x_1$から $x_2 (> x_1)$ になるように伸ばす場合，図2(B)のようにばねの弾性力に抗して外部から $f_{ex} = kx$との力を加えます．この外力による仕事は，

$$W (x_1 \rightarrow x_2) = \int_{x_1}^{x2} f dx = \int_{x_1}^{x^2} kx dx = \frac{1}{2} k x_2^2 – \frac{1}{2} k x_1^2 > 0 \tag{12}$$

となります．この仕事によって変化するエネルギーを $E_e$ とします．変化量は，

$$ \Delta E_e = W (x_1 \rightarrow x_2) \tag{13}$$

となり，基準点 $x_0= 0$ を予め決めておくと， $E_e$は図2(C)のように，

$$ E_p (x) = W(x_0 \rightarrow x) = \frac{1}{2} kx^2 \tag{14}$$

となります． ばねの伸びのみを考えた一次元の現象なので (3) に相当する式は，

$$ f_e = – \frac{d E_e}{dx} = -kx \tag{15}$$

となり，$E_e$ はポテンシャルエネルギーであり，弾性力 $f_e$ を保存力です．(4)より物体外部からされる仕事の微分は，

$$dW = – \frac{dE_e}{dx} = kx \tag{16}$$

となり，積分すると(11)になります．一次元なのでばねを $x_2$ から $x_1$ に戻す経路は，$x_1$ から $x_2$ に伸ばす経路のちょうど逆になります．往復する仕事は，$W(x_1 \rightarrow x_2) + W(x_2 \rightarrow x_1) = 0$ となり，(5)が成り立ちます．

2.2 運動エネルギー (kinetic energy)

並進運動エネルギー

物体の速度が変化した場合の並進運動エネルギー (translational kinetic energy) の変化を考えます．時刻 $t_1$ で位置 $\boldsymbol{x}_1$　[m] , 速度が $\boldsymbol{v}_1$ [m/s] であった物体が，時刻 $t_2$ で位置 $\boldsymbol{x}_2$ [m]， 速度 $\boldsymbol{v}_2$ [m/2] になったとします．物体の質量を $m$ [kg] とするとニュートンの第2法則により物体に作用する力は，

$$ \boldsymbol{f}_{ex} = m \frac{d \boldsymbol{v}}{dt} \ {\rm [N]} \tag{17}$$

と表すことができます．これに速度 $d \boldsymbol{x}/dt = \boldsymbol{v}$ [m/s] をかけます．

$$ \boldsymbol{f}_{ex} \cdot \frac{d \boldsymbol{x}}{dt} = m \frac{d \boldsymbol{v}}{dt} \cdot \boldsymbol{v} = m \boldsymbol{v} \cdot \frac{d \boldsymbol{v}}{dt} \tag{18} $$

これを時間について時刻 $t_1$ から $t_2$ まで積分します．

$$ \int_{t_1}^{t_2} \boldsymbol{f}_{ex} \frac{d \boldsymbol{x}}{dt} dt = \int_{t_1}^{t_2} m \boldsymbol{v} \cdot \frac{d \boldsymbol{v}}{dt} dt \tag{19}$$

この式の両辺は次のように変形できます．

$$ \int_{\boldsymbol{x}_1}^{\boldsymbol{x}_2} \boldsymbol{f}_{ex} \cdot d \boldsymbol{x} = \frac{1}{2} m |\boldsymbol{v}_2|^2- \frac{1}{2} m |\boldsymbol{v}_1|^2 \tag{20}$$

左辺は力 $f$ によって物体がされた仕事を表しています．したがって，外力によって物体速度が変化することにより，物体の並進運動エネルギーを $E_k$ とすると，

$$ \Delta E_k = W = \int_{\boldsymbol{x}_1}^{\boldsymbol{x}_2} \boldsymbol{f}_{ex} \cdot d \boldsymbol{x} = \frac{1}{2} m |\boldsymbol{v}_2|^2- \frac{1}{2} m |\boldsymbol{v}_1|^2 \ {\rm [J]} \tag{21}$$

だけ変化します.

$\boldsymbol{v} = 0$ のときを基準として $E_k=0$ とすると，

$$ E_k = \frac{1}{2} m |\boldsymbol{v}|^2 \tag{22} $$

となります．

2.3 エネルギー保存則

重力による位置エネルギーを考える場合には，重力を $f_{gz} = -mg$ に抗する力 $f_{ex} = – f_{gz}$ を外力とします．重力による運動エネルギーを考える場合には，外力は $f_{ex} = f_{gz}$ とします．物体を $z_1$ から $z_2 (> z_1)$ に持ち上げる場合，位置エネルギーと運動エネルギーの変化は，

$$ \Delta E_g = \int_{z_1}^{z_2} \left( -f_{gz} \right) dz \tag{23}$$

$$ \Delta E_k = \int_{z_1}^{z_2} f_{gz} dz \tag{24}$$

となり，

$$ \Delta E_g + \Delta E_k = 0 \tag{25}$$

となります．重力が作用する状態で物体が移動するという同じ現象ですが，位置エネルギーは増大し，並進運動エネルギーは減少します．両者を加えた総エネルギー (total energy) というものを定義すれば，これは変化しません．．

一般に (3) で表される保存力 $\boldsymbol{f}_p$ を外力として物体が $\boldsymbol{x_1}$ から $\boldsymbol{x_2}$ まで移動するとき，ポテンシャルエネルギーの変化は (4) より，

$$ \Delta E_p = \int_{\boldsymbol{x}_1}^{\boldsymbol{x}_2} (- \boldsymbol{f}_p) d \boldsymbol{x} \tag{26}$$

となり，運動エネルギーの変化は (20) より，

$$ \Delta E_k = \int_{\boldsymbol{x}_1}^{\boldsymbol{x}_2} \boldsymbol{f}_p d \boldsymbol{x} \tag{27}$$

となります．総エネルギーは，

$$ \Delta E_p + \Delta E_k = 0 \tag{28}$$

と変化しません．これをエネルギー保存則 (law of energy conservation) といいます．

3. 熱力学的なエネルギー

まず，熱力学的な系の状態変数とエネルギーにどのようなものがあるか列記します．状態変数の内容については次節の「基本概念」で紹介します．

3.1 系の状態変数と熱力学的なエネルギー

系の熱力学的な状態 (thermodynamic state of the system) は，

• 体積 (volume) $V \ {\rm [m^3]}$
• 圧力 (pressure) $p \ {\rm [Pa]}$
• 温度 (temperature) $T \ {\rm [ K]} $
• エントロピー (entropy) $S \ {\rm [J/K]}$
• 物質の量 – モル数 (number of moles) $N \ {\rm [mol]}$ や 質量(mass) $M \ {\rm [kg]}$）
• 化学ポテンシャル (chemical potential) $\mu {\rm [J/mol]}$

の組み合わせで表すことができます．これらを状態変数 (state variables) と呼びます．系の状態を決定するためにはこれら全てが必要なのではなく，独立なものの組み合わせを選択すると残りは系の性質から連動しての決定されます．選択した組み合わせの状態変数を独立変数 (independent variables) といい残りを従属変数 (dependent variables) といいます．熱力学的なエネルギー (thermo dynamic energy) には独立変数の組み合わせにより，

• 内部エネルギー (internal energy) $U[S,V,{\boldsymbol N}]$
• ヘルムホルツエネルギー (Helmholtz energy) $F[T,V,{\boldsymbol N}]$
• ギブスエネルギー (Gibbs energy) $G[p,T,{\boldsymbol N}]$
• エンタルピー (enthalpy) $H[p,S,{\boldsymbol N}]$

があります．これらの独立変数の組み合わせを自然な熱力学変数の組み合わせといい，本記事では鉤括弧内 [ ] に入れて表現します．その他の組み合わせの場合は $U(T,V,{\boldsymbol N})$ のようにふつうの括弧 ( ) に入れて表現します．内部エネルギー $U$ は，単にエネルギーとよばれることもあります．多成分の物質を含む系の物質量は，

$${\boldsymbol N} = (N_1,N_2, \cdots, N_n) \tag{29}$$

のように成分ごと物質量 $N_1, N_2, \cdots, N_n $ を並べたベクトルとなります．

3.2 単一成分かつ単一相の物体の熱力学的状態と熱力学的なエネルギー

単一成分かつ単一相の物体の場合は質量が固定されているので，独立な状態変数は，体積 $V$，圧力 $p$，温度 $T$，エントロピー $S$ のうち2個です．熱力学的なエネルギーと自然な熱力学変数の組み合わせは，

• 内部エネルギー $U[S,V]$
• ヘルムホルツエネルギー $F[T,V]$
• ギブスエネルギー $G[p,T]$
• エンタルピー $H[p,S]$

となります．

4. 基本概念

エネルギーの説明を始める前に，状態変数である物質の量，体積，圧力，温度，エントロピーなど必要となる基本概念を整理します．そして，熱力学的状態や状態量の概念を明確にします．というのは，これらは新しい理論や法則が発見される度に見直されている概念であり，現代でも我々の認識が一致してるとはいいきれないからです．そして熱量と内部エネルギーの関係を説明します．

4.1 物質の量

我々が物質の量をどのようにして測っているのかということを通して，量の概念の変遷を概観します．

4.1.1 重さと体積

古来より，物体に含まれる物質の量は，重さ (weight) または体積 (volume) で表されてきました．重さは天秤を使って物体の重力の大きさを測定することによって得られます．液体（水や油など）や固体の粒子（穀物など）の体積は枡などの空間的な大きさの決まった容器を使って計量できます．空間的大きさの測定法は様々ですが，最終的には球の直径や直方体の縦・横・高さなどの測定できる長さの積から求められます．枡で測れる体積は枡の縦・横・高さを $\Delta x, \Delta y, \Delta z$ とすると次のように表せます．

$$ V = \sum \Delta x \Delta y \Delta z \tag{30}$$

1630年代ごろ，ガリレオは，圧縮した空気を詰めて栓をしたガラス瓶の重さと栓を外して空気の一部が逃げていった後のガラス瓶の重さの差から，空気のような気体にも重さがあることを発見しました．以来，液体や固体だけでなく気体も重さを測定する対象となりました．気体の体積は力を加えることにより簡単に変化します．体積は物体に含まれる物質の量を表すものではなく物体の状態である，すなわち状態変数のひとつだと考えられるようになります．前述したように，系の概念では，質量も状態変数のひとつです．日常生活では現代でも体積による量の見積もりが行われています．

相加性と計量

重さ $M_1$ の物体と重さ $M_2$ の物体を合わせて1つの物体を構成すると，重さは $M_1 + M_2$ となります．同様に，体積 $V_1$ の物体と体積 $V_2$ の物体を合わせて1つの物体を構成すると，体積は $V_1 + V_2$ となります．このような性質を相加的 (additive) といいます．物体を系に置き換えても同様です．我々は，この性質を利用して天秤が釣り合うときの分銅の重さの和で重さを測定し，枡の容積と杯数の積で体積を測定します．

4.1.2 質量

1687年にニュートンの第２法則 (Newton’s second law) が発見されると，物体に作用する重力 (gravity force) と物体の質量 (mass) の概念が分離されます．我々が重さとして測定している量は重力という力の大きさであり，重力 $f_g$ [N] は質量 $M$ [kg] と重力加速度 $g {\rm [m/s^2]}$ の積で表されます．

$$ f_g = M g \tag{31}$$

物体に含まれる物質の量は質量 $M$ で表されます．地球表面付近では重力加速度 $g$ はほぼ一定だとみなせるので重力 $f_g$ の大きさを測定することにより質量 $M$ を計算することができるのです．

物体を重力加速度が異なる環境に持っていくと，重さは変化しますが質量は変化しません．力学の範囲では，質量が物体に含まれる物質の量を表します．このように物理学では，新しい法則が発見されるたびに基本的な量の概念が大きく変わることがあります．

1774年，ラボアジエによって質量保存則（化学反応の前後で反応に関与する物質の質量は変化しない）が発見され，反応物と生成物を含んだ物体から成る閉じた系で，質量が普遍的な物質の量であると考えられるようになりました．

4.1.3 化学当量

1660年頃，ボイルは，古代ギリシャ哲学的の先験的な元素論を否定し，元素（物質の構成要素，element）が実験による分析によって経験的に決められるべきであるという考えを示しました．以来，様々な化合物の分析が行われ，1789年のラボアジェの「化学原論」では33種の元素が挙げられています．

ある元素一定量と結合したり置換したりする他の元素の量を化学当量 (chemical equivalent) といいます．化学当量の考え方はウェンツェルによって提案され，1777年に最初の酸と塩基の当量表が発表されています．それとは独立に，リヒターは，1792-1794年の著作で酸と塩基の中和に関して質量の比が一定となること示しています．1799年に，プルーストは定比例の法則（化合物を構成する元素の質量の比が一定である）を発見しました．1803年に，ドルトンは倍数比例の法則（同量の元素と化合する元素の質量は簡単な整数比となる）を発見しました．以後，質量保存則，定比例の法則，倍数比例の法則などに基づいて，化学反応に関与する物質の量的関係を説明する化学量論 (stoichometry) が発展します．化学当量は，一定量の基準となる元素（炭素や酸素）と化学反応するの量に基づいて，様々な元素の物質の量を表現します．

4.1.4 原子量・分子量とモル数

1805年，ドルトンは倍数比例の法則を説明するために原子説（atomic theory, まだ仮設）を唱え，水素に対する元素の相対質量（質量比）を示す原子量表を発表しました． 1808年，ゲーリューサックは気体反応の法則（気体の化学反応において，体積比が簡単な整数比になる）を発見しました．1811にアボガドロは，アボガドロの仮説（同一温度，同一圧力，同一体積の気体には同じ数の粒子が含まれる）を発表し，この粒子を分子 (molecule)とよびました．アボガドロの仮説は1860年のカールスルーエ国際会議におけるカニッツァーロの解説以降に受け入れられ，化学当量と原子量や分子量の概念が明確に区別されるようになります．現在 (1961年以降) では、炭素の同位体である炭素12の質量を12とした場合の原子や分子の相対質量を原子量 (atomic weight) や分子量（molecular weight) と呼んでいます。

分子が実在することは，1905年のアインシュタインのブラウン運動の研究と1909年のアインシュタイが導出した式を使ったペランの実証実験などで明らかになります．そして，原子や分子の存在が実証されたことにより，現代ではアボガドロの仮説はアボガドロの法則と呼ばれています．

国際単位系 (SI) の物質量であるモル数の旧定義（2019年5月２０日より前まで）では，分子量にグラムをつけた質量に含まれる分子の量を１mol としていました．これは炭素12に対する原子や分子の相対質量を基準とした物質の量の定義です．

4.1.5 アボガドロ定数とモル数

アボガドロの法則に従い、温度 0 ℃ (273.15 K)、圧力 1 気圧 (101325 Pa)、22.4 l (リットル) の気体にはアボガドロ数 $6.02214076 \times 10^{23}$ の分子が含まれます。アボガドロ数の旧定義は 0.012 kg の炭素に含まれる原子数でしたが，現在(2019年5月２日以後）では正式に定数となりアボガドロ定数と呼ばれるようになりました．

国際単位系 (SI) の，現在（2019年5月20日以後）の物質量の定義では，アボガドロ定数個の要素粒子（原子，分子，イオン，電子など）の量を 1 mol とします．つまり，モル数の定義は，単純に原子や分子の数を基準とする物質量に変更されました．

4.1.6 熱力学と原子や分子

熱力学が確立された19世紀の中頃は，原子や分子の存在は実証されていません．熱力学には当時の仮説である原子説や分子説を前提としなくても成立する普遍的な理論体系があります．現代において熱力学の知識を利用する立場では，どのようなに立場に基づいて物質の量が定義されていてもあまり問題なく，相互に変換することが可能です．しかし，熱力学を理解しようとするときに，原子や分子の存在を前提する統計物理的な知識を使用すると，論理の展開（どのような議論から何が導出されたのか）がわかりにくくなるので注意が必要です．

4.1.7 系の化学的平衡

(1) 相転移

液体の水と氷の系を考えます．このように不均質な系が境界面で区別される複数の部分から構成され，各部分の中が均質である場合，各部分を相 (phase) といいます．複数の相から成る系を多相系 (pollyphase system) といいます．固体の部分を固相 (solid phase)，液体の部分を液相 (liquid phase) といいます．水の場合の水蒸気のように気体の相を気相 (gas phase) といいます．水の融解や蒸発のように１つの相から別の相へ移る現象を相転移 (phase change) といいます．

(2) 化学反応

酸素，水素，水蒸気が混合した系を考えます．このように複数の物質から成る系を多成分系 (multicomponent system) といいます．この系では次のような化学反応 (chemical reaction) が起こります．

$$ \mathrm{ 2H_2 + O_2 \rightleftharpoons 2H_2 O } \tag{32}$$

(3) 化学的平衡

多相系や多成分系は，相転移や化学反応が起こると相や成分の物質の量が変化します．順方向と逆方向の相転移や化学反応が釣り合って物質量が変化しないことを化学的平衡 (chemical equilibrium) といいます．化学平衡状態では，相や成分の化学ポテンシャル (chemical potential) という示強変数が互いに等しくなります．示強変数の意味については次の圧力のところで述べます．また，化学ポテンシャルの説明は後回しにしたいと思います．本記事では，まず単一成分かつ単一相の物体について議論し，その後で多相系や多成分系の話題に移りたいと考えています．化学ポテンシャルについてはそのときに詳細を明らかにする予定です．

4.2 圧力

4.2.1 圧力の発見

1643年，トリチェリによって水銀柱を使用した空気の圧力（pressure）の測定が行われ，我々の身の回りに圧力（大気圧）が作用していることが明らかになり始めました．また，この測定によって真空 (vacuum) も発見されました．この測定方法は次のようなものです。一端を閉じた 1m のガラス管に水銀を満たし、それを水銀が入った容器に倒立させると、ガラス管内の水銀は容器の水銀の液面から76 cm の高さまで下降してとまります。ガラス管の 76 cm より上の部分の空間は真空になります。この状態は、容器内の水銀の表面の高さで，空気が容器内の水銀の表面を下方に押す単位面積あたりの力と水銀柱の単位面積あたりの重力が釣り合っている状態です。この空気が水銀の表面を押す単位面積あたりの力が空気の圧力です．圧力は物体の表面に垂直方向に作用する力です．単位面積当たりの力で表し，${\rm Pa}$ (パスカル) = ${\rm N/m^2}$ という単位を使用します．圧力は物体の表面に作用する力の測定と面積の測定によって実測可能です．

4.2.2 パスカルの原理

1663年のパスカルによるパスカルの原理（静止している流体に伝わる圧力はどこでも等しくなる）の発見により、流体（液体や気体）がもつ圧力の性質が明確になります。圧力は，静止した流体全体に一様に分布します．圧力は静止した流体のかたまり全体に対して１つの値をもち，全体に共通な状態を表します．

パスカルの原理は次のように考えることができます．流体の内部を仮想的に切り取り，その部分に作用する力を考えます．流体や弾性体を扱う連続体力学では，これを面積力（surface force, 断面に作用する力）と体積力（body force, 体積に比例する力）に分けます．代表的な体積力は重力です．単位面積あたりの面積力を応力 (stress) といいます．応力は面に対して垂直な法線応力 (normal stress) と面に沿った方向の接線応力 (tangential stress) に分解できます．流体が静止している場合，この切り取った部分の断面に対して，次のことが言えます．面積力に対して体積力が無視できる場合を考えると，

• 接線応力はゼロとなる．
• 法線応力は全ての面で同じ大きさになる．

そもそも，静止状態において接線応力がゼロとなることが流体の定義です．接線応力がゼロでなければ流動状態になります．法線応力の大きさが同じになることは，面積力の釣り合いから導かれます．これらより，静止した流体内部を任意の多数の部分空間に分割すると，すべての部分で法線応力の大きさと表面の圧力は等しくなります．これを静止流体の内部の圧力として定義すると，流体の圧力は，流体の内部に一様に分布することになります.

静止状態の圧力は，静水圧　(hydrostatic pressure) や静圧 (static pressure) ともよばれます．なお，法線応力が圧力と等しくなるのは流体が静止している場合のみです．流体が流動している場合には，法線応力には圧力だけでなく動圧 (dynamic pressure) や粘性応力 (viscous stress) の法線成分などが加わります．

体積力が無視できない場合は，面積力と体積力の釣り合いから体積力の方向に圧力の分布が生じます．重力による圧力分布の例としては，高い山の上で気圧が低いことや，水圧が水深とともに大きくなることが挙げられます．トリチェリの実験でも水銀柱内部に重力による圧力分布があり，水銀柱が静止状態は，76 cm の深さ水銀の圧力と大気圧が釣り合った状態です．

4.2.3 圧力の下限

流体では，真空の状態が圧力の下限であり，これをゼロとします．固体では，表面に加わる力や法線応力が正のとき圧力，負のときは張力 (tension)とよび，両者を区別します．

4.2.4 力学的平衡状態を表す状態変数としての圧力

トリチェリの圧力測定では，混じり合わない流体である水銀と空気を接触させたとき，水銀と空気の圧力が釣り合うところで両方の流体の境界面が静止しました．自由に動くピストンを介して接触する２つの流体の場合でも同様で，圧力が釣り合う位置でピストンが静止します．２つの流体で圧力が釣り合った状態を機械的平衡または力学的平衡 (mechanical equilibrium)といいます．流体を任意の数の部分に仮想的に分割したものを系と考えると，静止した状態では分割したすべての部分の圧力が等しくなります．これを系の力学的平衡状態 (mechanical equilibrium state of the system) といい，圧力の値ひとつで系全体の力学的平衡状態を表すことができます．このような意味で，圧力は系の力学的平衡状態を表す状態変数であるといいます．

4.2.5 示強変数

系の大きさを変えても値の変わらない量を示強的 (intensive) であるといい，示強的な変数を示強変数 (intensive variable) といいます．圧力は示強変数の一つです．このような説明の教科書は多いのですが，系の大きさを変えるという概念があいまいです．系の大きさ（あるいは量）は質量や体積で表現されます．これらは独立した状態変数ですから，質量を固定して体積を変化させるような操作も可能です．この場合一般的には圧力は変化します．

私は次のように考えます．系または物体を仮想的に任意の数の部分空間に分割したとき，分割したどの部分で測定しても同じ値をとるような量を示強的であるといいます．つまり，系の大きさを変えるという部分を系を仮想的に部分空間に分割すると読み替えます．静止状態の圧力が示強変数であることはパスカルの原理が根拠となります．但し，体積力が無視できない場合は，体積力による効果を差し引いた圧力のみを考えます．

4.3 温度

温度は，物質の量や体積，圧力などと異なり，力や長さなどの力学的な測定で直接的は得られる量ではありません．まず，我々の肌感覚として温かさや冷たさなどがあります．温度の概念は，これをどのようにして定量化するか，また定量化の方法によってどのように再定義するか，という経緯を経て形成されてきました．

4.3.1 熱平衡状態と温度

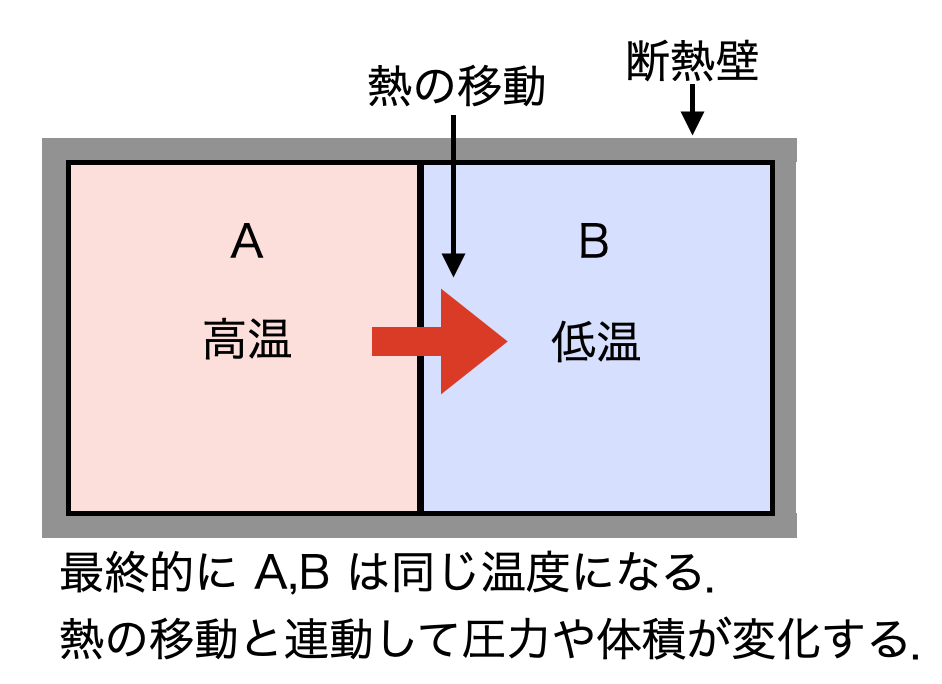
温度が異なる２つの物体を熱的に接触させると高温の物体から低温の物体に何かが移動します．日常的に，我々はこの移動するものを漠然と熱と呼んでいます．熱そのものは見えませんが，我々は物体の体積や圧力が変化することを測定することによって熱が移動したことを認識することができます．つまり，温度の変化と熱の移動，そして物体の体積や圧力の変化は連動しています．時間が経過すると最終的には物体の圧力や体積の変化は止まります．この状態を熱平衡 (thermal equilibrium)といいます．我々は，熱平衡に達した２つの物体の温度は等しいと定義します．つまり2つの物体を接触させて熱が移動する状態なら温度が異なる，熱が移動しない状態なら温度が等しいとします．重さの計測で天秤に分銅をのせて天秤が振れるかどうかを判断するように，温度の計測では熱的に接触させた物体の体積や圧力が変化するかどうかを判断します．

純粋に２つの物体の熱平衡状態を得るには，対象とする２つの物体を外部の環境から断熱した状態にしなければなりません．2つの物体を環境に接触させておくと環境と同じ温度になってしまうためです．2つの物体は，断熱することによって外界と異なる温度（異なる熱平衡状態）になることができます．

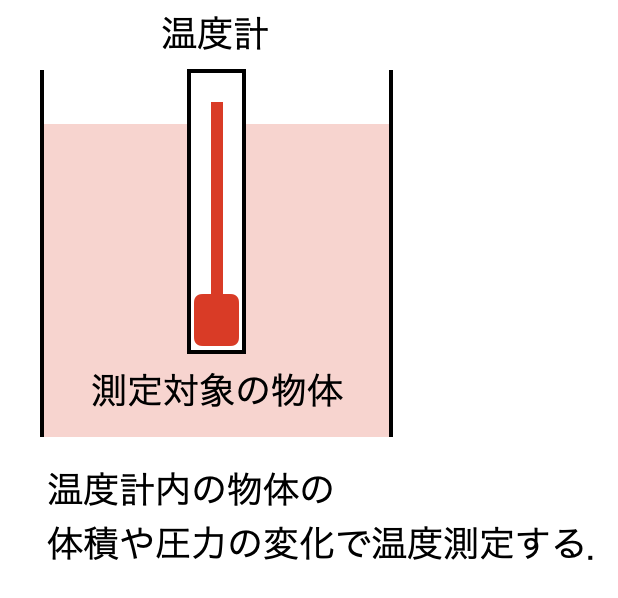
熱が移動する現象は，対流を伴わずに物体内部を熱が伝わる熱伝導，物理的に接触した物体間を熱が伝わることや流体の対流によって熱が搬送されることを含んだ総合的な熱の移動を表す熱伝達，物体どうしは非接触であるが電磁波の形で熱が伝わる放射伝熱などがあります．熱的な接触はこれらを全て含む概念です．上図は簡略化して象徴的に描いた概念図です．

また上図では断熱壁を使って物体を断熱した状態を表現しています．これも，実際の実験では，熱伝導を抑えるために熱伝導率の小さい物質（断熱材）で覆う（熱伝導シールド），放射熱伝達を抑えるために反射率の高い物質で覆う（熱放射シールド），熱を伝える物質の無い真空で外界から隔離する（真空断熱）など，いろいろな技術が用いて必要なレベルの断熱効果が得られるように工夫します．

4.3.2 熱平衡状態を表す状態変数としての温度

2つの物体の系の熱平衡断状態の考えを拡張し，断熱された系を仮想的に任意の数の部分空間に分割した場合を考えます．十分時間が経過すると全ての部分の温度が同じになります．この状態を系の熱平衡状態 (thermal equilibrium of the system) といいます．系の熱平衡状態は1つの温度で表すことができます．このような意味で，温度は系の熱平衡状態を表す状態変数です．分割したどの部分で測定しても値が変わらないので，温度も圧力と同様に示強変数です．

4.3.3 経験的温度と状態方程式と熱力学第０法則

体積や圧力の変化量は物体を構成する物質によって異なります．そこで，基準となる物質を入れた温度計を作り，温度計と測定対象の物体が熱平衡になったときの温度計内の物体の体積や圧力の変化量で温度を表します．このようにして定められた温度を経験的温度 (empirical temperature) といいます．詳細は述べませんが，現代でもよく使われている経験的温度には，ファーレンハイトが1724年に提唱したファーレンハイト温度（華氏温度） ${\rm ^\circ F}$，セルシウスが1742年に考案し1752年頃までに目盛りが逆転されたセルシウス温度（摂氏温度） ${\rm ^\circ C}$ などがあります．セルシウス温度は水の融点を基準 ($0 {\rm ^\circ C}$)とし沸点 ($100 {\rm ^\circ C}$) のまでの間を100分割する刻み幅をもつ温度です．

経験的温度が測定できるためには次のようなことが要請されます．

• 物質や系に状態方程式の関係が存在すること．
• 熱平衡の推移律が成立すること．

(1) 状態方程式

状態方程式 (equation of state) は，物体に含まれる物質の量と温度，圧力，体積の関係を表します．状態方程式は物質ごとに異なり，残念ながら熱力学の範囲では導出できません．実験により経験的に得るか，分子運動論などの統計物理的なモデルから与えられます．

(2) 熱平衡の推移律（熱力学第０法則）

熱力学第０法則 (0th law of thermodynamics) は次のように表されます．

「物体Aと物体Bが熱平衡にあり，物体Aと物体Cが熱平衡にあれば，BとCは熱平衡にある．」

物質が異なると状態方程式も異なります．熱平衡の推移律を前提とすることにより，固体のようにほとんど体積や圧力が変化しないか，変化を測定するのが難しい物体でも，他の物質を使って作った温度計を使って共通の目盛りで温度が測定できます．

4.3.4 理想気体温度

理想気体の状態方程式

$$ pV = n R T \tag{33}$$

は，ボイル・シャルルの法則（気体の圧力 $p$ が体積 $V$ に反比例し，温度 $T$ に比例する）とアボガドロの仮説に基づく気体のモデル式です．$R = 8.31446262 \ {\rm [J/(mol \ K) ]}$ は気体定数 (universal gas constant)，$n$ はモル数です．質量をベースにして物質量を表すと，単位質量 (1 kg) 当たりの理想気体の状態方程式は，

$$ pV = R_s T \tag{34}$$

となります．$R_s = R / M_m \ {\rm [J/(kg \ K)]}$ は比気体定数 (specific gas constant) とよばれ，$M_m \ {\rm [kg/mol]}$ はモル質量（1モル当たりの質量) です．

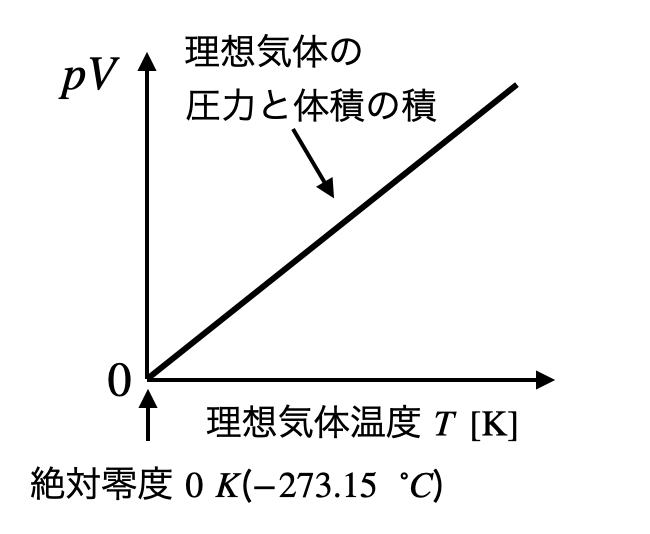
理想気体は多くの気体の高温低圧の状態を精度良く再現することができます．理想気体のモデル式を使用して低温定圧の状態を外挿すると体積と圧力の積がゼロのとき温度が最低となります．これを絶対零度 ($-273.15 {\rm ^\circ C}$) といいます．理想気体温度は絶対零度を基準とし，セルシウス温度のように1気圧(101325 Pa) の水の融点と沸点の間を100分割する刻み幅をもつ温度です．

4.3.5 熱力学的温度

経験的温度は，温度計内の物質の特性（状態方程式）に依存するため普遍的なものではありません，理想気体温度は現実には存在しな気体のモデルを基礎としています．どちらも普遍的な温度目盛りではありません．

1824年に，熱機関の効率を研究していたカルノーは，カルノーサイクルという熱機関のモデルを考案し，カルノーサイクルの効率 $\eta$ が物質の種類によらず低温 $T_1$ と高温 $T_2$ の２つの熱源の温度だけの関数の比 $\phi(T_2) / \phi(T_1)$に依存することを証明しました．カルノーサイクルは理想化されたモデルですが，その効率は現実の熱機関の効率の普遍的な上限を表すものです．

$$ \eta = 1- \frac{Q_2}{Q_1} =1 – \frac{\phi(T_2)}{\phi(T_1)} \tag{35}$$

まだ説明に必要な内容を紹介しきれてないのでここでは詳細は述べませんが，1848年にケルビンは，このカルノーサイクルの効率を使って定義される熱力学的温度を提唱しました．熱力学的温度は物質の種類に依存しません．

$$ \eta = 1- \frac{T_2}{T_1} \tag{36}$$

熱力学的温度は, K (ケルビン) を単位記号とし，１つの基準点（水の三重点の温度，273.16 K）を定義することによって決定されます． また，理想気体を用いてカルノーサイクルを構成することによって，理想気体温度と熱力学的温度が一致することが確かめられています．熱力学の範囲では，この熱力学的温度が普遍的な温度目盛りです．本記事では基本的は，この熱力学的温度を使用します．他の温度を使用するときには単位記号で区別します．

4.3.6 統計物理に基づく温度

原子や分子の存在を前提とする統計物理では，まずエントロピーを定義し, エントロピーから温度が導入されます．現代(2019年５月20日以降)の国際単位系(SI)では統計物理の考え方が導入され，水の三重点温度ではなくボルツマン定数 ($k=1.380649 \times 10^23 \ {\rm J/K}$) から温度 ${\rm K}$ (ケルビン) が定義されています．

4.4 熱力学的状態と状態量

3.1 で系の状態変数として，体積，圧力，温度，エントロピー，物質の量，化学ポテンシャルを挙げたました．そして，これらのうち独立なものの組み合わせで熱力学的状態が表現できると述べました．もう少し詳しく見ていきます．ただし，エントロピーと化学ポテンシャルについては，まだ説明していないのであまりふれません．

4.4.1 熱力学的状態の定義

熱力学の教科書では，「系の状態が変化する」という言葉がよく出てきます．そもそも系の状態とは何であり，どうやって変化を知るのかわからなければ話になりません．我々が取り扱う状態は熱力学的平衡状態 (thermodynamic equilibrium state) です．これを単に熱力学的状態 (thermodynamic state) ということもあります．これは系が次の３つの平衡に達した状態です．

• 力学的平衡
• 熱平衡
• 化学的平衡

まず，化学的平衡ですが，これは系に含まれる物質の量が変化しない状態です．単一成分物質から成る閉じた系は，物質の量は一定なので化学的平衡状態にあるとみなせます．多成分系では，成分ごとの物質の量が全て変化しない状態が化学的平衡状態で，これは成分の数だけの物質の量で表すことができます．化学ポテンシャルも化学的平衡状態を表す示強変数ですがまだ考えません．

上に示した３つの平衡を直接表現する状態変数は，力学的平衡状態は圧力，熱的平衡状態は温度，化学的平衡状態は化学ポテンシャルです．しかしながら，これらは示強変数であり，これらだけの組み合わせでは，系の量を表現することはできません．系の量を表現するためには，状態変数の組み合わせの中に次に示す示量変数を加える必要があります．

4.4.2 示量変数

体積やエントロピーは，示強変数を固定すれば，物質の量に比例します．このような性質を示量的 (extensive) といい，このような性質をもつ状態変数を示量変数 (extensive variables) といいます．質量やモル数など，物質の量そのものも示量変数です．よく熱力学の教科書では，単に系の大きさに比例する性質のことを示量的と定義していますが，大きさを表す質量と体積は独立に変化させることができるので，私はあいまいな表現だと思います．

4.4.3 現時点で選べる熱力学的状態変数

力学的な方法で測定可能な状態変数は，物質の量と体積と圧力です．これらと状態方程式から温度を確定することができます．エントロピーと化学ポテンシャルを説明していないので現時点では，熱力学的状態は，物質の量と，体積・圧力・温度の3つのうち２つによって確定できると考えてよいでしょう．

4.4.4 状態量

熱力学的な状態量 (quantity of state) は，基本的には物体や系の熱力学的状態のみで値が確定される量を表します．逆に熱力学的状態のみで確定されない量を非状態量といいます．非状態量は１つの熱力学的状態から別の熱力学状態に移るときの変化量が移るときの経路に依存します．

質量 $m$ の物体の場合，熱力学的状態は圧力 $p$，温度 $T$，体積 $V$ のうち２つで表現できます．$(p,V)$ を状態変数に選んだ場合に，1つの熱力学的平衡状態 $(p_A, V_A)$ から別の熱平衡状態 $(p_B, V_B)$ へ移る任意の２つの経路 $C_1$ と $C_2$ を考えると, 関数 $X(p,V)$ が状態量であれば，

$$ \int_{C_1} dX = \int_{C_2} dX \tag{37}$$

となります．経路というと空間的な道すじをイメージすると思いますが，$C_1,C_2$は状態変数 $(p, V)$ で表される状態空間 (state space)上の道すじと考えることができます．$(p_A,V_A)$ から $C_1$ の経路を通って $(p_B, V_B)$ へ移動し，$(p_B,V_B)$ から $C_2$ と逆の経路で $(p_A,V_A)$ に戻ると，

$$ \oint dX = \int_{C_1} dX – \int_{C_2} dX = 0 \tag{38}$$

となります．$X(p,V)$ の全微分は，

$$ dX = \left( \frac{\partial X}{\partial p} \right)_V dp + \left( \frac{\partial X}{\partial V} \right)_p dV \tag{39}$$

と表されます．(37),(38),(39) の関係は，ポテンシャルエネルギーにおける (6),(5),(4) の関係と同じです．

(39)のように$X(p,V)$ が全微分で表されるための必要十分条件は，

$$ \frac{\partial}{\partial V} \left( \frac{\partial X}{\partial p} \right)_V = \frac{\partial}{\partial p} \left( \frac{\partial X}{\partial V} \right)_p \tag{40}$$

です．

いったんある物理量が熱力学的な状態量であることがわかると，その状態量を状態変数の1つとして使用することが可能となります．

．